Hilbert space approximation for Gaussian processes in Numpyro

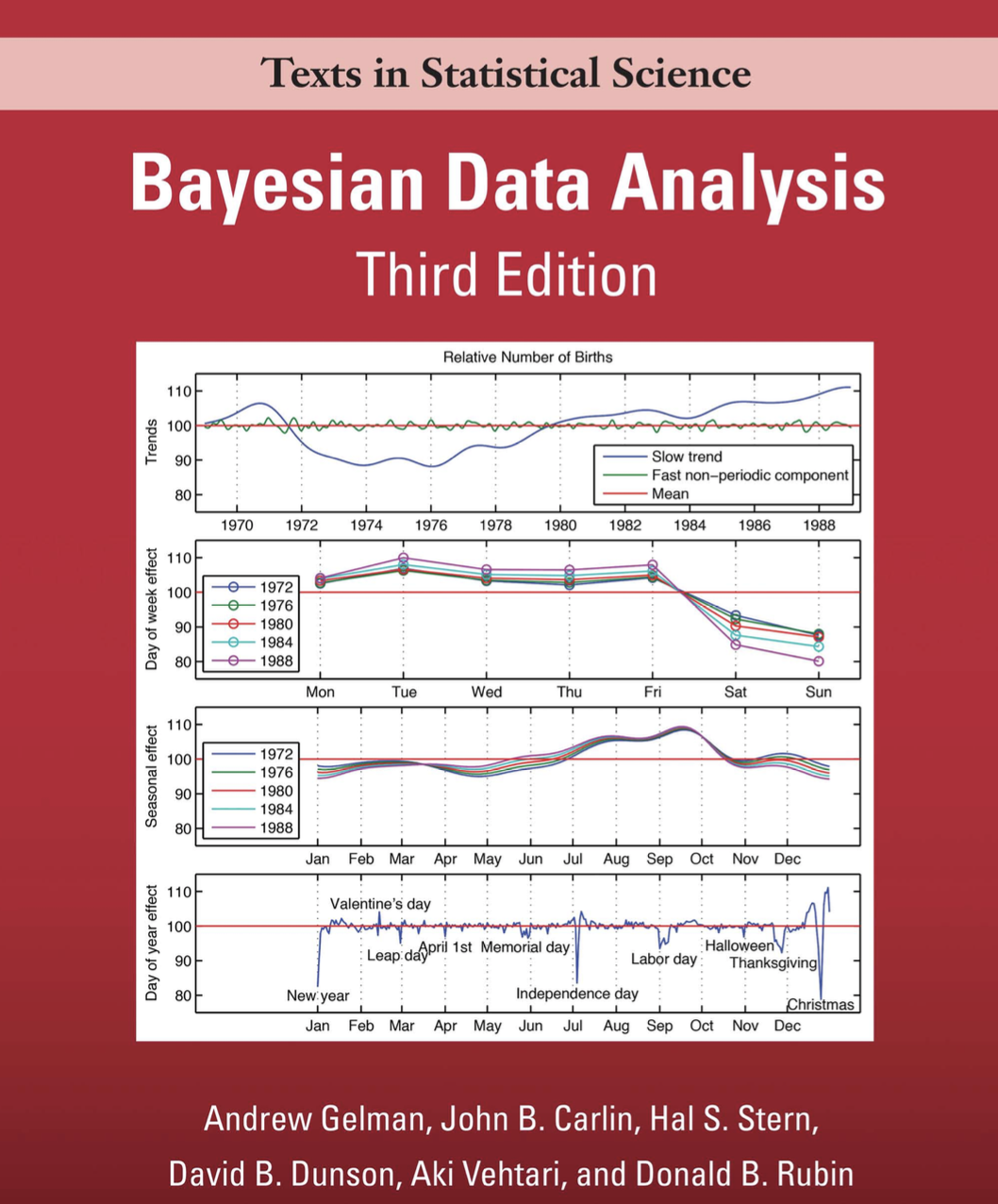
The book I used for learning about Bayesian inference has a very provocative plot on the cover

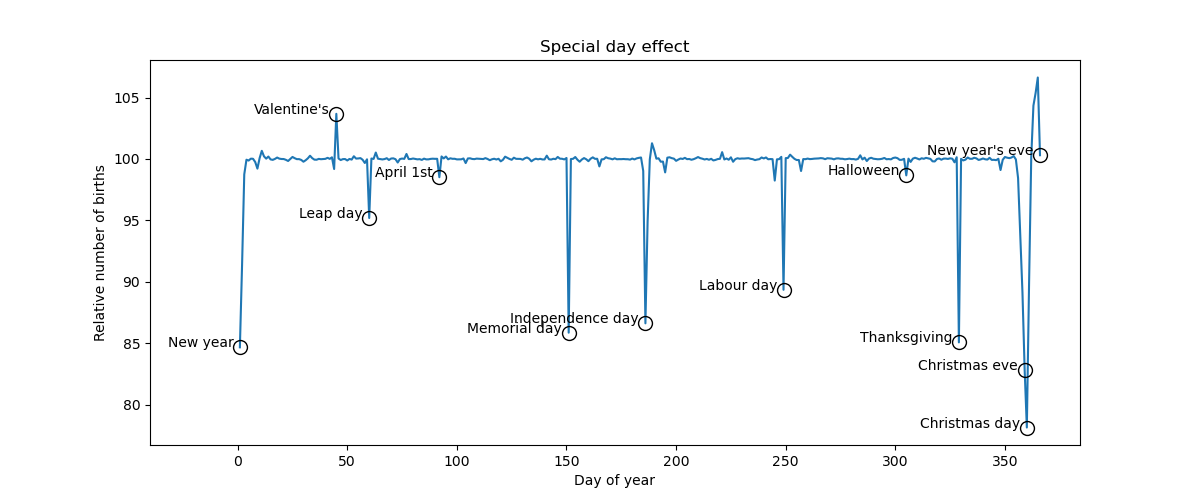
The plot might seem innocent at first but trust me, its place on the front cover is well deserved. The plot is about the daily number of births in the US. Its goal is to address a hypothesis first raised in this paper by Becca Levy, Pil Chung, and Martin Slade that was published in the Social Science & Medicine journal. Simply put the claim of the paper was that

more babies are born on Valentine’s day and fewer are born on Halloween.

But more or less compared to what? The average of course. The problem is that the average number of daily births is something that has changed over the years, it changes over the months and during the week. And these changes are complex, not easily captured with a simple model. The original paper addresses the question in a rather pedestrian way, using a frequentist ANOVA. If you want a rigorous Bayesian answer you will have to make it all the way to chapter 23 (out of 25) of the famous BDA3: Gaussian processes.

Using a beefy Gaussian process the different components are extracted: the slow varying trend, the year seasonality, the weekly effect with slowly increasing magnitude, and the effect of every single day of the year. The effects of Valentine’s Day and Halloween (and other special days) emerge (see plot at the top).

But the mathematical discussion behind this model hides a huuuuge caveat. Fitting a GP to this dataset (with roughly 7000 observations) would require computing the inverse of a 7000x7000 matrix – and inverting it hundreds of times if we’re doing full Bayes. That’s just a no-go. So how on earth did they fit this model?

My hunt for their code was rather frustrating. I ended up here which apparently runs in a piece of software called GPStuff and not in Stan like the rest of the examples in the book. I really couldn’t be asked to learn GPStuff so for many months this had been the end of the road for me.

Until recently, the amazing Aki Vehatri linked this case study in his blog. In there, he shows how one can use Stan and R to do full Bayes on this dataset via a Hilbert space approximation for Gaussian processes. The mathematical details behind the approximation are explained in this article.

Of course, I’m not going to repeat here all that Aki and collaborators have already shared. But I’ve taken the time to port their code over to Python and Numpyro. Hopefully, you’ll find it useful. Personally, I’m glad that approximate GPs are now part of my toolkit and that I can put an end to chapter 23 :)

Here’s the code: https://github.com/omarfsosa/hsgp