A simple example of ordinal regression
The Queen’s Gambit came out and I binged the whole thing because, you know, that’s what we do in the times of Covid. I really enjoyed it, actually, but once Beth Harmon was out of the way, the chess-stats questions started to flow. In particular, there were 2 scenes in this show that left me thinking (SPOILERS AHEAD!):
- First, when Mr. Sheibel is starting to teach Beth how to play, he always plays the white pieces. It’s only after a few games that he tells Beth that she can play white pieces too. So how much does playing white increases one’s probability of winning?
- And second, when Beth goes to sign up for her first tournament, the organisers give her a bit of a hard time because she does not have an Elo rating. So, how do Elo ratings determine someone’s probability of winning?
No doubt there’s been tons of research about these questions already, and I bet quick google search will suffice to get an answer. But that’s no fun. Instead, I’ve downloaded a bunch of games from the FIDE World Cups and I’ve decided to write my own model to answer my questions. Of course, FIDE world cups are far from a representative sample of an average chess game, so all results I’ll show here only apply to FIDE world cup games (or perhaps other games outside the world cup but that involve players just as skilled and similar playing circumstances).
After dealing with some formatting issues, here’s the data in the always-friendly csv format:
| date | white_id | black_id | white_elo | black_elo | result | |
|---|---|---|---|---|---|---|
| 0 | 2019-09-10 | 9100075 | 8603677 | 1954 | 2811 | 0-1 |
| 1 | 2019-09-10 | 24116068 | 10207791 | 2780 | 2250 | 1-0 |
| 2 | 2019-09-10 | 8504580 | 623539 | 2284 | 2774 | 0-1 |
| 3 | 2019-09-10 | 5202213 | 6501311 | 2767 | 2387 | 1-0 |
| 4 | 2019-09-10 | 4902980 | 4168119 | 2407 | 2776 | 0-1 |
| ... |
Elo Based model
To answer my questions, I will fit a model that tries to predict the outcome of the game based on the Elo difference between the players. Of course, simply saying that the player with higher Elo would win is not good enough. Such approach would miss the fact that playing white pieces might give you an edge. For example, in this post, FiveThirtyEight explain how they use an Elo based model for predicting the outcome of NFL games (a sport very similar to chess). Their model is such that: \begin{align} P_{win} = \frac{1}{1 + 10^{\frac{\mathrm{-EloDiff}}{400}}} \label{eq:elo} \tag{1} \end{align} As it is, this model assumes that the game is “fair”, having both teams playing under equal circumstances. FiveThirtyEight then makes adjustments to the Elo of each team depending on other factors like if the team is playing at home or not, etc. Now, I cannot simply use this model because
- I don’t happen to be a chess expert unfortunately, so I don’t know by how much I should change the Elo of players if they have white pieces. This is precisely my first question.
- Equation \(\eqref{eq:elo}\) tells me the Elo difference is being modelled as a logistic distribution (because the CDF is a logistic function). I don’t know why this system has a problem with the Normal distribution, so I’ll use a logistic distribution too just to be on the safe side. However, I doubt that \(\log(10)/400\) would also be the right scale for Chess. So I will need to learn this from my model.
- And finally, it’d seem to me that the above model would predict a tie only when both teams have the same Elo score. Ties are way more frequent in FIDE games than they are in NFL (I guess not that similar after all), so to account for this I need to turn the logistic regression model into an ordinal regression model.
That leaves me with the following model:
\begin{align} P_{lose}(A) &= 1 - 1 / (1 + 10^{-(\alpha + E_A - E_B - c_1)/\sigma}) \newline P_{draw}(A) &= 1 / (1 + 10^{-(\alpha + E_A - E_B - c_1)/\sigma}) - 1 / (1 + 10^{-(\alpha + E_A - E_B - c_2)/\sigma})\newline P_{win}(A) &= 1 / (1 + 10^{-(\alpha + E_A - E_B - c_2)/\sigma})\label{eq:elo2} \tag{2}, \end{align} where \(\alpha\) is a term representing first move advantage and the cutpoints \(c_1\) and \(c_2\) help me to account for the 3 possible outcomes.
Ordinal regression in Stan
I’m going to fit this model in Stan (what else?). The model code is quite simple and it looks like this:
Perhaps the only remarkable aspect of it is the fact that I’m not using 2 independent parameters for the cutpoints but, instead, I make one the negative of the other. I do this because I want to enforce that any unbalance in the game is taken into account only by the first-move-advantage term.
To build the model, I first put the data in the right shape and then pass it to Stan. I will also use ArViz to visualize my chains:
Looking at the inference data I see that all my chains have mixed nicely on my first attempt1
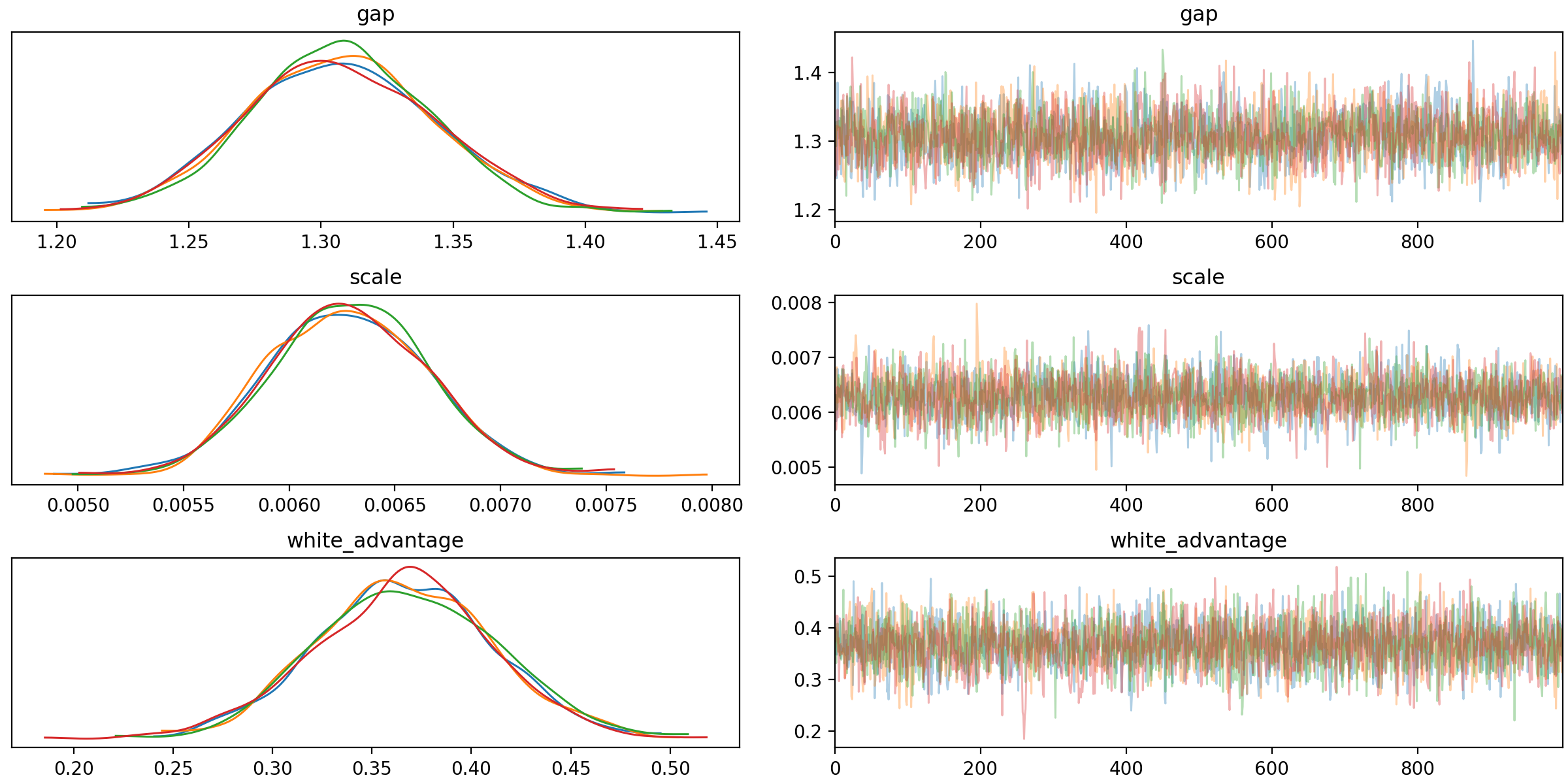
And the mean estimates of my parameters are:
| parameter | mean | std |
|---|---|---|
| white_advantage | 0.366611 | 0.044193 |
| scale | 0.006281 | 0.000375 |
| gap | 1.307304 | 0.035150 |
So, according to this model, if you’re playing white pieces against someone of the same Elo rating on a FIDE world cup, then
\begin{align} P_{win}(A) &= \mathrm{logit}^{-1}(0.36 - 1.31) &\approx 28\% \newline P_{draw}(A) &= \mathrm{logit}^{-1}(0.36 + 1.31) - \mathrm{logit}^{-1}(0.36 - 1.31) &\approx 56\% \newline P_{lose}(A) &= 1 - \mathrm{logit}^{-1}(0.36 + 1.31) &\approx 16\% \end{align}
And if chess were a fair game without first move advantage then we would have
\begin{align} P(win) = P(lose) &= \mathrm{logit}^{-1}(- 1.31) &\approx 21\% \newline P(draw) &= 2 * \mathrm{logit}^{-1}(-1.31) &\approx 58\% \end{align}
This means that playing white pieces increases your chances of winning by 7%, and decreases your chances of losing by 5%. To answer my second question I just need to plot equations \(\eqref{eq:elo2}\) with the mean estimates. Here are my plots including the advantage for playing white pieces:
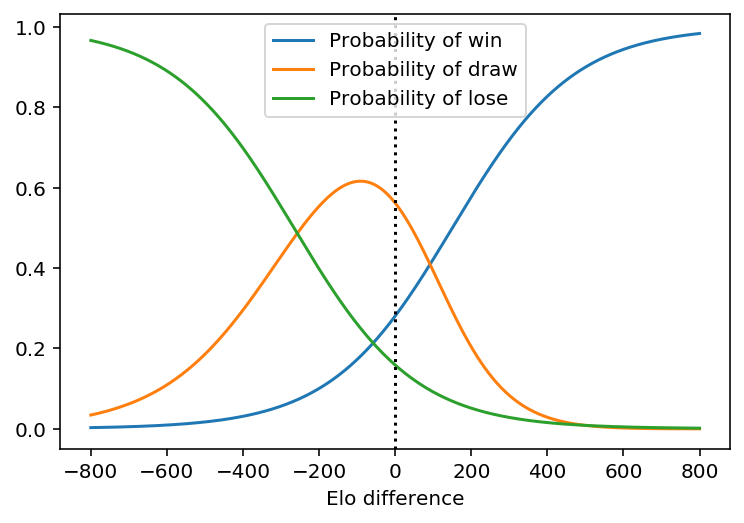
These results look sensible to me given my very limited experience in chess world cups, so I’m going to call it a day. If you’d like to learn more about ordinal regression, I recommend you read this post by Mike Betancourt.
-
Maybe it was not my first attempt but you have no way of knowing that so… ↩